Provas 'impossíveis' do teorema de Pitágoras publicadas por alunos do ensino médio: WebCuriosos
O que começou como uma pergunta bônus em um concurso de matemática do ensino médio resultou em surpreendentes 10 novas maneiras de provar a antiga regra matemática do teorema de Pitágoras.
É longo foi reivindicado impossível usar a trigonometria para provar o que é efetivamente um teorema fundamental para a trigonometria. Isso cai no falácia lógica de pensamento circular tentando provar uma ideia com a própria ideia.
“Não existem provas trigonométricas porque todas as fórmulas fundamentais da trigonometria são baseadas na verdade do teorema de Pitágoras”, disse o matemático Elisha Loomis. tinha escrito em 1927.
Mas duas colegas do ensino médio nos EUA, Ne'Kiya Jackson e Calcea Johnson, alcançaram o “impossível” durante o último ano do ensino médio em 2023.
Agora eles publicaram esses resultados junto com mais nove provas.
“Houve muitos momentos em que nós dois quisemos abandonar este projeto, mas decidimos perseverar para terminar o que começamos”, disseram Jackson e Johnson. escreva no papel deles.

O teorema de Pitágoras descreve a relação entre os três lados de um triângulo retângulo.
É incrivelmente útil para engenharia e construção e foi usado por humanos séculos antes de a equação ser atribuída a Pitágoras, inclusive, alguns afirmam, na construção de Stonehenge.
O teorema é uma lei fundamental no campo da trigonometria, que trata essencialmente das relações entre lados e ângulos dos triângulos. Você provavelmente se lembra de ter a equação a2+b2=c2 perfurado em você na escola.
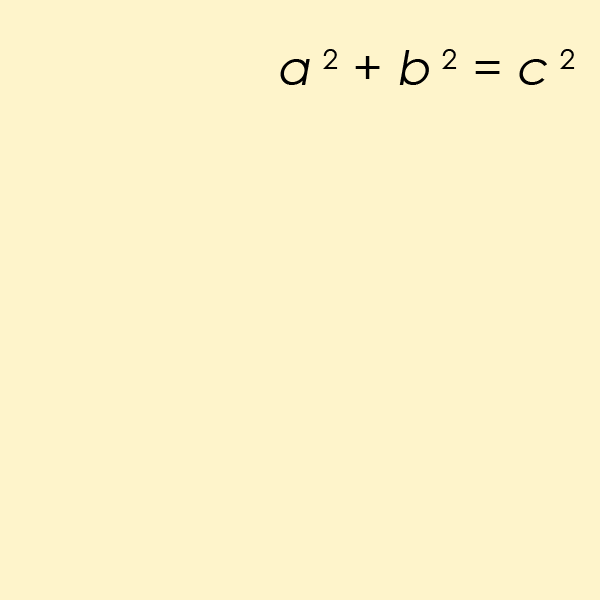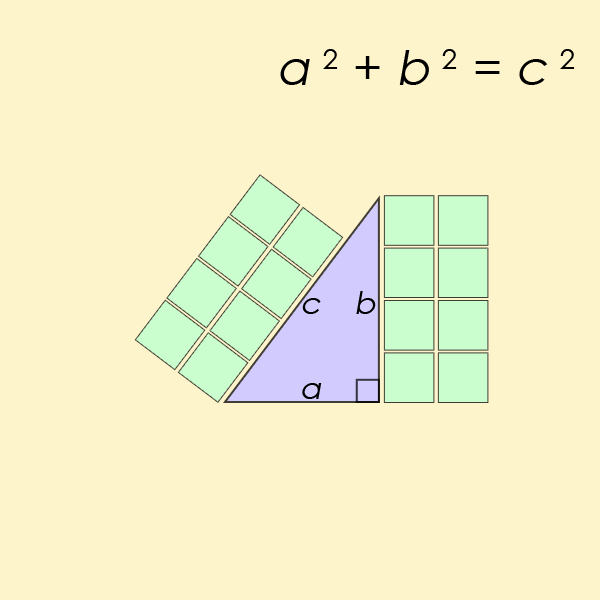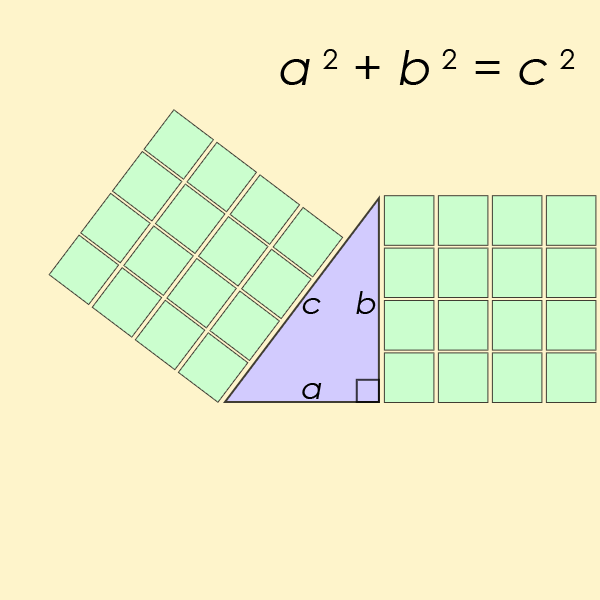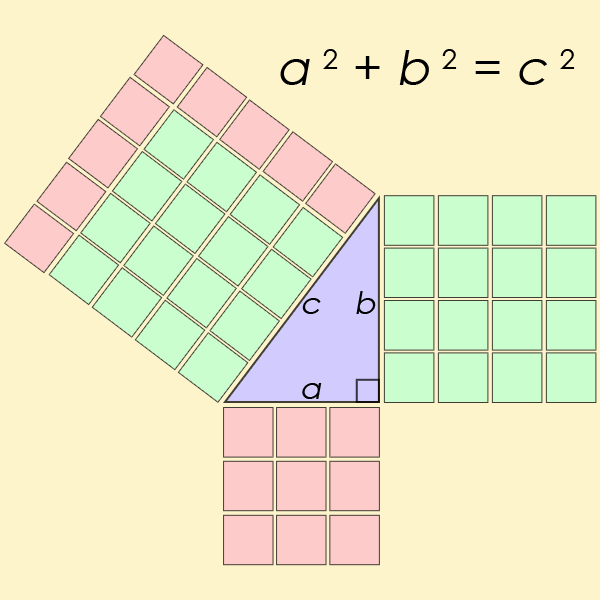
“Os alunos podem não perceber que duas versões concorrentes de trigonometria foram estampadas na mesma terminologia”, explicar Jackson e Johnson.
“Nesse caso, tentar entender a trigonometria pode ser como tentar entender uma imagem onde duas imagens diferentes foram impressas uma sobre a outra.”
Ao desemaranhar essas duas variações relacionadas, mas diferentes, Jackson e Johnson foram capazes de encontrar soluções inovadoras usando o Lei dos Senosevitando o pensamento circular direto.
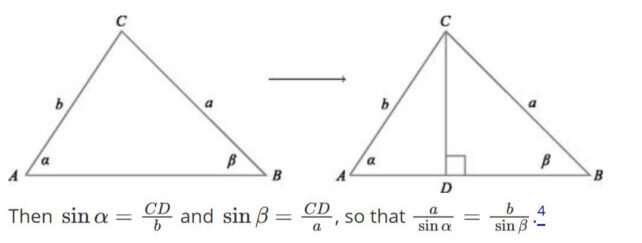
Jackson e Johnson descrevem esse método em seu novo artigo, embora observem que a linha entre trigonométrica e não trigonométrica é um tanto subjetiva.
Eles também apontam que, segundo sua definição, dois outros matemáticos experientes, J. Zimba e N. Luzia, provaram o teorema também usando trigonometria, desafiando afirmações anteriores de que isso era impossível.
Em uma de suas provas, os dois alunos levaram a definição de cálculo com triângulos ao extremo, preenchendo um triângulo maior com sequências de triângulos menores e usando cálculo para encontrar as medidas dos lados do triângulo original.

“Parece nada que eu já tenha visto”, disse Álvaro Lozano-Robledo, matemático da Universidade de Connecticut contado Nikk Ogasa no Science News.
Ao todo, Jackson e Johnson fornecem uma prova para triângulos retângulos que têm dois lados iguais e outras quatro provas para triângulos retângulos com lados desiguais, deixando pelo menos mais cinco para “o leitor interessado descobrir”.
“Ter um artigo publicado tão jovem é realmente alucinante”, diz Johnson, que agora estuda engenharia ambiental. Jackson agora está estudando farmácia.
“Seus resultados chamam a atenção para a promessa de uma nova perspectiva dos estudantes na área”, diz Della Dumbaugh, e.diretor-chefe da revista em que são publicados.
Esta pesquisa foi publicada no Mensal Matemático Americano.