
Matemático finalmente resolve o antigo problema do sofá em movimento: WebCuriosos
Os matemáticos geralmente não são o primeiro ponto de contato no dia da mudança. E realmente, por que deveriam ser? Por quase 60 anos, eles não conseguiam nem dizer se o seu novo e sofisticado sofá de três lugares conseguiria chegar ao seu apartamento.
Jineon Baek pode mudar de ideia sobre isso. O entusiasta de combinatória e geometria da Universidade Yonsei, na Coreia, acaba de lançar uma prova de 100 páginas neste mesmo problema, resolvendo uma das questões mais urgentes do Universo para que todos possamos fazer melhores escolhas de móveis antes de ficarmos presos no topo da escada do terceiro andar.
Em 1966o matemático austro-canadense Leo Moser formalizou um problema que assola a humanidade desde um esgotado Australopithicus primeiro ficou nos confins de uma caverna com uma carcaça de gazela de aparência confortável que simplesmente não se movia mais.
Superficialmente, parece simples. Qual é o maior objeto bidimensional que consegue contornar com sucesso um canto em forma de L?
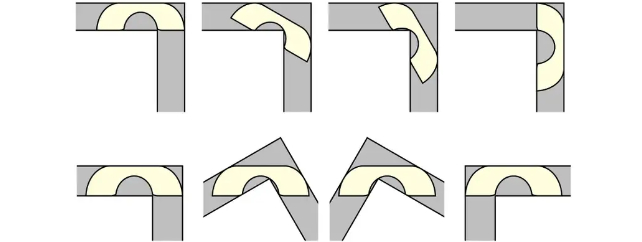
Para um corredor com uma unidade de largura, uma cadeira com uma unidade quadrada é um passeio no parque. Por outro lado, uma unidade de dois quadrados perfeitamente retangular obviamente ficará presa. Esqueça mais nada – agora ele mora no corredor.
Mas e se for alguma coisa única da IKEA com o nome de um personagem do Senhor dos Anéis e o formato de um receptor de telefone antigo?
Apenas dois anos depois que Moser lançou o desafio, o matemático britânico John Hammersley encontrou um sofá que consiste em um semicírculo dissecado separado por um quadrado com uma mordida de semicírculo removida (onde três amigos podem tocar os joelhos desajeitadamente enquanto falam matemática) poderia ter 2,2074 unidades de área e ainda apenas faça isso na esquina.
Hammersly também definido um limite superior para o design – nada maior que 2,8284 poderia passar.
Quase um quarto de século se passou antes que um estudioso da Universidade Rutgers chamado Joseph Gerver sugerisse um redesenho sutil no sofá de Hammersly, arredondando algumas bordas com arcos extras e encontrando uma forma que adicionasse frações ao limite anteriormente inferior para reivindicar o o tamanho máximo do sofá é uma fração acima de 2.2195 unidades.
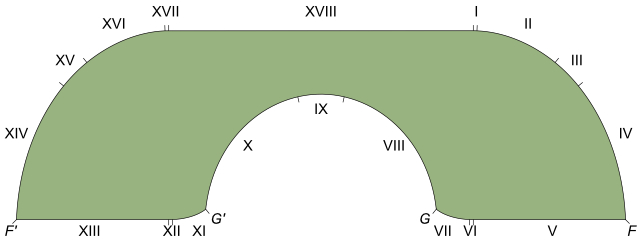
Gerver mostrou com sucesso que sua solução era localmente ótima, estabelecendo um novo limite inferior para a área máxima. Em outras palavras, a sua solução foi a melhor dentro das condições limitadas definidas por aquela forma.
Sem uma fórmula universal para formatos de sofás que descreva todas as dimensões possíveis dos móveis, no entanto, é difícil provar que um sofá um pouco maior com curvas sutilmente diferentes pode não funcionar.
Em 2018o matemático do Santa Fe Institute, Yoav Kallus, e Dan Romik, da Universidade da Califórnia, Davis, usaram um esquema assistido por computador para mostrar que o sofá poderia ter até 2,37 unidades.
Para esta última prova, Baek aplicou um pouco de magia matemática conhecida como função injetiva mapear formas bem-sucedidas do sofá de Gerver, bloquear propriedades-chave antes de expandi-las através de dimensões cada vez maiores para provar de uma vez por todas o quão grande um sofá do tipo Gerver poderia ser.
Com certeza, 2.2195 unidades são o rei dos sofás para um corredor de 1 unidade de largura e um canto em forma de L, tal como Gerver propôs em 1992.
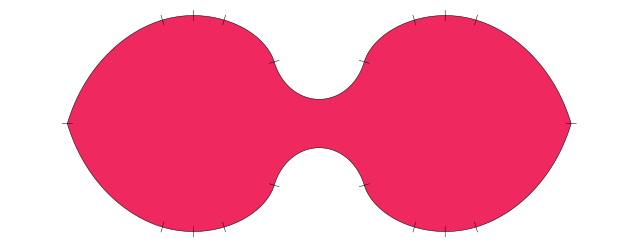
Embora ainda não tenha sido revisada por pares, a solução de Baek pode ser a palavra final sobre o problema do sofá, pelo menos neste cenário. Se você tiver um segundo canto para virar na direção oposta, recomendamos um formato chamado sofá ambidestro de Romik.
Agora disponível no corredor 13 da IKEA, ao lado da mesa da cozinha de Gimli.
Esta pesquisa está disponível no servidor de pré-publicação arXiv.




