Este padrão secreto escondido no Sudoku vai te surpreender: WebCuriosos
Por um lado, o sudoku é uma maneira simples e divertida de passar o tempo e manter o cérebro funcionando – mas vá mais fundo e alguns padrões matemáticos diabolicamente inteligentes se revelam. O mais recente que nos surpreendeu? O Anel Phistomefel.
O Anel Phistomefel (ou Teorema Phistomefel) é lindamente ilustrado em um vídeo de Numerófilo que você encontrará incorporado abaixo.
Tem o nome de um construtor de sudoku alemão e, além de ser um padrão de dígitos superinteligente, também pode ajudá-lo a resolver esses quebra-cabeças mais rapidamente no futuro.
frameborder=”0″ permitir=”acelerômetro; reprodução automática; gravação na área de transferência; mídia criptografada; giroscópio; imagem em imagem; web-share” referrerpolicy=”strict-origin-when-cross-origin” permitir tela cheia>
Se você é novo no sudoku – cada tabuleiro de jogo é composto de nove quadrados iguais, cada um dividido em nove quadrados menores em um arranjo 3 x 3. Cada linha e coluna do tabuleiro, bem como cada quadrado 3 x 3, devem ser preenchidos com os dígitos de 1 a 9, sendo cada dígito usado apenas uma vez.
Existem mais padrões aqui: cada linha, coluna e quadrado 3 x 3 contém, portanto, dígitos que somam 45, por exemplo. No entanto, Phistomefel encontrou um padrão mais profundo que é muito mais impressionante.
De acordo com o princípio do Anel Phistomefel, os 16 quadrados que circundam o quadrado central 3 x 3 sempre conterão os mesmos dígitos – em cada quebra-cabeça de sudoku – que aqueles nos quatro quadrados 2 x 2 nos cantos do tabuleiro do quebra-cabeça. Você pode ter uma ideia melhor disso na imagem abaixo:
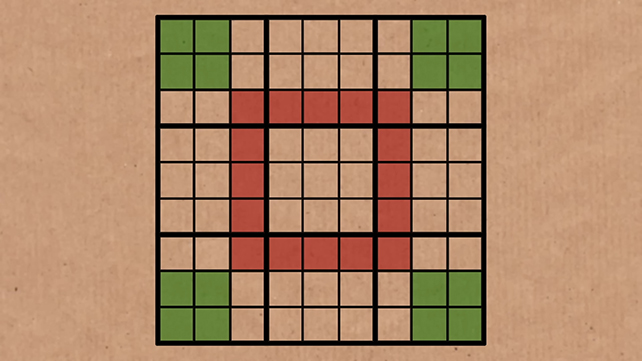
Mesmo que não saibamos em que ordem eles estão, sabemos que todos os dígitos nos quadrados verdes correspondem exatamente a todos os dígitos nos quadrados vermelhos. Pode levar algum tempo para entender, mas é lindo em sua simetria.
O Anel Phistomefel funciona por causa de algo chamado Teoria da Equivalência de Conjuntos.
Imagine a coluna central em verde e a linha do meio em vermelho de um tabuleiro de sudoku, sobrepostas no meio – o quadrado central em azul. Sabemos que tanto a linha como a coluna contêm os dígitos de 1 a 9, em qualquer ordem.
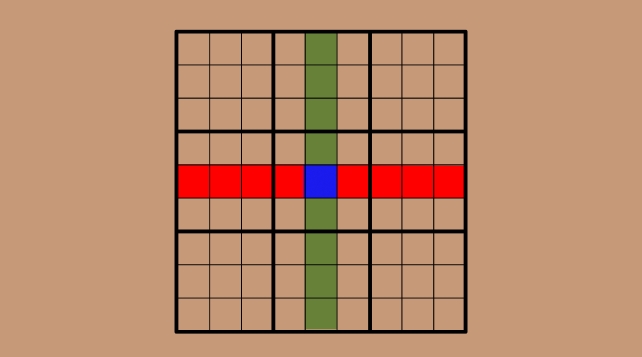
Agora, retire o quadrado azul do meio, onde está a sobreposição – cortando o meio da linha e da coluna. Não sabemos qual é esse dígito, mas sabemos que o mesmo dígito foi removido da linha e da coluna e, portanto, os dígitos restantes também corresponderão.
O Phistomefel Ring é essa ideia em letras grandes, com oito conjuntos de 1 a 9 dígitos em vez de apenas dois. Há mais números envolvidos, mas a ideia é a mesma: os quadrados que não se sobrepõem devem conter os mesmos dígitos. Você pode ver os oito conjuntos abaixo, coloridos em duas grades separadas:
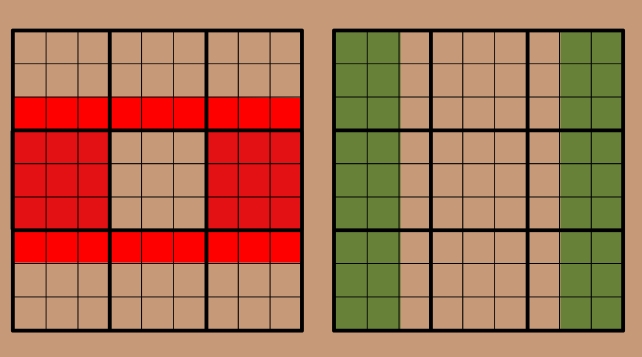
Os conjuntos em vermelho são duas linhas de cores vivas e dois quadrados 3×3 maiores no meio esquerdo e no meio direito da grade do sudoku. Os conjuntos em verde estão em duas colunas de cada lado da grade.
Na próxima imagem, os conjuntos são mostrados na mesma grade, com os quadrados sobrepostos coloridos em verde mais escuro:
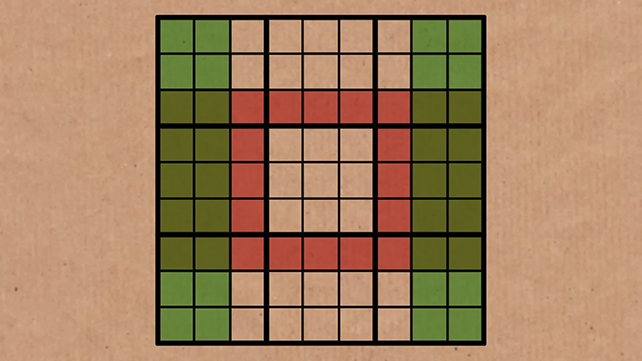
Retire essas sobreposições e os blocos restantes em verde e vermelho devem ter os mesmos números restantes.
Agora vamos ver quantos padrões de sudoku mais podemos encontrar…